In this page I will explore more in details how the Aequilibrium code has been developed.
FISHES RENDER
First we need to graphically render the fishes.. this is done with a simple piece of code taken from a mouse tail example in the processing sketchbook folder. A series of circles are drawn from a starting point. Each circle is smaller that the previous and is traslated a few pixel in order to create a tail effect. Than we added some alpha transparency and linked the circle starting point to our fish position.
These lines are in the main Fish class function called update()
for(int i=1; i
mx[i-1] = mx[i];
my[i-1] = my[i];
}
mx[num-1] = posx;
my[num-1] = posy;
render();
}
The last line render(); call the separate function render that draws the fish:
void render() {
for(int i=0; i
fill (80, 100, 150, 20);
ellipse(mx[i], my[i], i, i);
}
}
FISHES MOVEMENTS
In order to create a fish and to make it moving we need to know a random starting position for the fish and an orientation angle.
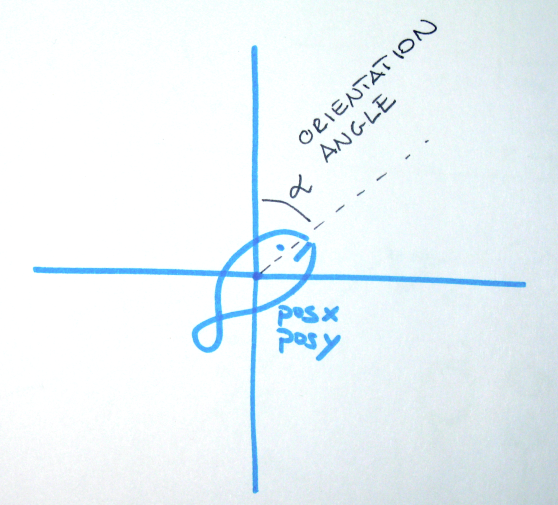
We use the orientation angle to control the x and y speed of the fish because x and y increments need to change differently depending on the direction the fish is following. To do this we use the sine and cosine function. If we consider a circle with a radius of 1 and a given angle alpha we know that sine(alpha) is equal to the x value of the segment drawn from the circle’s center (with alpha angle) and that cosine(alpha) is equal to the same segment y value.
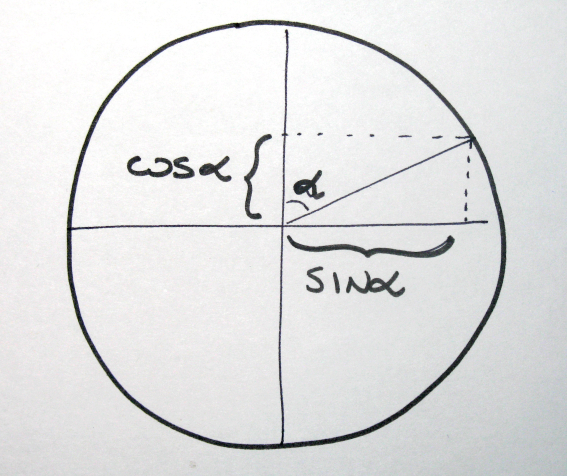
We can than use these two values as incremental factors to control the x and y speed of the fish. Here is the code:
yalpha = sin(radians(fishangle-90+inview));
xalpha = cos(radians(fishangle-90+inview));
posx = posx + (xalpha*speed) + tailmovx/2;
posy = posy + (yalpha*speed) + tailmovy/2;
In the last two lines you can see two unknown variables named tailmovx and tailmovy. I created then to add the tail a fish-like movement.
They work in this way:
//XTAIL MOVEMENT////
float xtail() {
float xcostail;
float m = (millis())%360;
xcostail = cos(radians(m));
return(xcostail);
}
//YTAIL MOVEMENT////
float ytail() {
float ycostail;
float m = (millis())%360;
ycostail = sin(radians(m));
return(ycostail);
}
I declare a float variable called m containg a milliseconds counter. The counter starts when the fish is rendered for the first time and return to 0 value everytime it reaches 360 (this is done with the modulo function %360 at the end).
I calculate the sine of this value (of course cosine for the y value) and obtain another factor to add to the x and y speed.. this value changes every millisecond giving the tail movement.
RANDOMNESS
Fishes apparently move in a rondam way.. to simulate a bit of randomness I used this little if cycle:
int l = floor(random(0,12));
if ( l == 6) {
fishangle = fishangle + random(-40,40);
}
The application while running keeps generating random integer numbers between 0 and 12.. only when the generated number is equal to 6 (but it could any other number in the range) the fish orientation angle changes instantly.
INTELLIGENT FISHES
Fishes need to become aware of a “target” position in order to try to avoid it or to follow it. To do this I use two basic functions: the absolute distance between the fish ant the target and the difference between the fish’s angle and the target’s angle calculated with the arctan function.
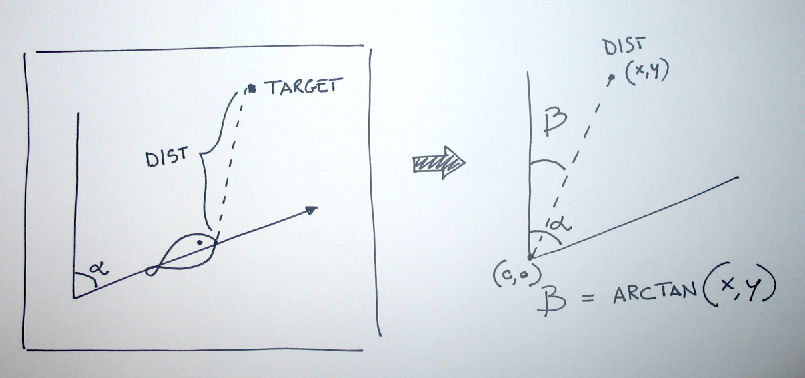
Arctan is a quite complex function (at least becouse it is limitied between -PI/2 and PI/2).. you can find more explanation here in wikipedia. Basically it is the inverse function that calculates the angle from the tanget segment. In this case the application calculates the absolute distance between the fish and the target. If the distance is less than a arbitrary value (in this case 350px) the insight function is called.
The insight function uses the target x and y position to calculate the arctan and gets the target angle value. Than a series af if cycle check the difference between the fish’s angle and the target’s angle and progressively adjust the fish’s angle in order to reduce the difference (if we want the fish to get closer to the target) or to increase the difference (in we want the fish to avoid the target).
Unfortunatly as I said before arctan is a difficult function and we needed more if cycles to control the position. In this case we simply added more controls checking case by case how the values where changing.. even if this is not a real mathematical approach.
if (distance < 350) {
insight(fishangle,a,viewangle,turnspeed);
}
//INVIEW/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void inview(float myangle, float targetangle, float viewangle, float tempturnspeed) {
float d = 0;
float leftSD = (myangle-viewangle);
float rightSD = (myangle+viewangle);
if (targetangle > leftSD && targetangle < rightSD) {
if (targetangle > myangle) {
fishangle = (fishangle - tempturnspeed)%360;
}
else if (targetangle < myangle) {
fishangle = (fishangle + tempturnspeed)%360;
}
}
else if (( leftSD < 0) && (targetangle > (myangle+180))) {
float temptargetangle = targetangle - 360;
if (temptargetangle > leftSD && temptargetangle < rightSD) {
fishangle = (fishangle + tempturnspeed)%360;
}
}
else if (rightSD > 360) {
targetangle = targetangle + 360;
if (targetangle > leftSD && targetangle < rightSD) {
fishangle = (fishangle - tempturnspeed)%360;
}
}
else {
}
}
These are only a few bites of the aequilibrium application with some suggestions about the way we solved our problems. There are probably other possible solutions and the code is not so precise. Probably the best way to understand these pieces of code is to analyze them with processing, modifying them and playing with them. It is possible that the same functions can be used with other objects.
I want to thank Durrell Bishop for his help with this code.
> Download .zip folder with aequilibrium code.
> Experience Aequilibrium with your mouse.
> Watch the prototype video on youtube.
> Next.